

Research Interests
My past and present research interests are mostly about the theoretical understanding of the large-scale structure of the Universe. This topic emerged in the seventies at the instigation of Zeldovitch etc. and is of prime importance to answer two burning issues of theoretical astrophysics:
• How galaxies form and evolve? And in particular how much important is their large-scale environment in shaping them?
• What are the constituents and the laws that drive our Universe? In particular, what is dark matter, this non-luminous form of matter that represents 85% of the matter content of the Universe? What is responsible for the acceleration of the cosmic expansion? Is the theory of General Relativity failing at some scales?
With the advent of large surveys (SDSS, Planck and in the coming years Euclid, LSST, . . .), astronomers are now in an era of high-precision cosmology with huge amounts of data at hand. In order to deal with those data and learn more about our Universe, there is a real need for theorists to build tools that could extract as much fundamental information as possible from those data. In particular, it means being able to do predictions (from first principles!) in the non-linear regime of structure formation, tackle systematic effects like redshift space distortion, galaxy bias, intrinsic alignments of galaxies, etc. All my research focuses on those challenges because they are – as its name implies – challenging but also because they combine my love of mathematics and my long-standing fascination to the mysteries of the cosmos.
Project |01




Galaxy clustering in the large-deviation regime
In the very early stages of my research experience, I learned perturbation theory and how it can be “renormalized” and “regularized” so as to do predictions as far as possible in the non-linear regime. In particular, I contributed to write a fast public code that computes the dark matter power spectrum at “two-loop” order in the regularized perturbation theory.
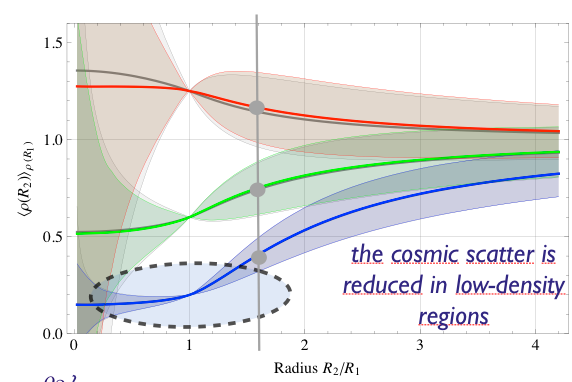
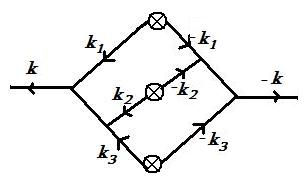
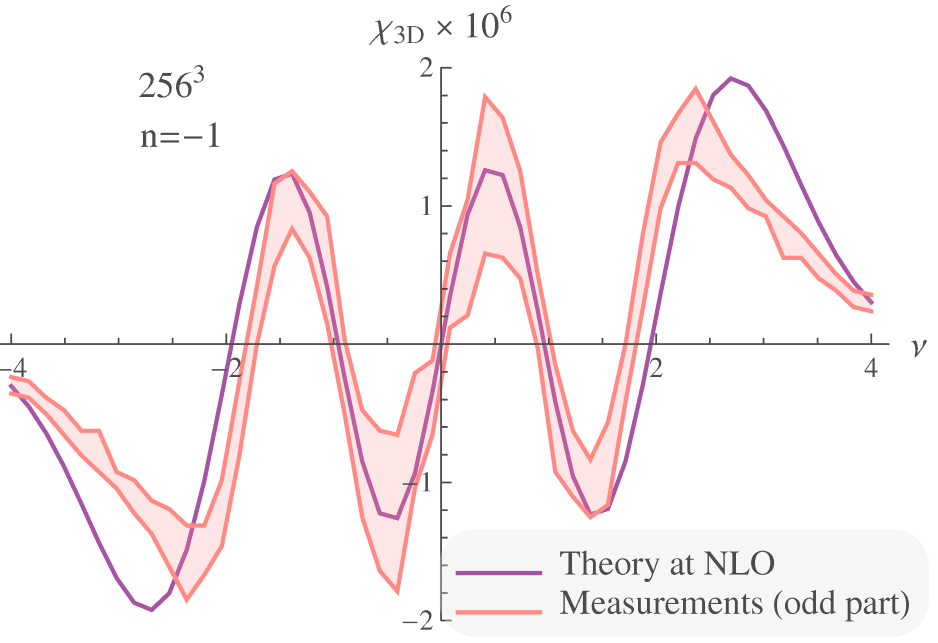
Since then, I have also been being interested in the so-called “count-in-cell” statistics which is a very simple observable (counting galaxies in concentric spheres) but thanks to beautiful mathematics (large-deviation theory) allows to do analytical predictions in a mildly non-linear regime (beyond what is usually accessible by standard PT-based statistics). Some slides are available here on this topic.
Project |02



Topology of the large-scale structure
During my PhD, I learned about cosmic-web classification. Defining precisely what is a filament, a wall, a void is still a debated issue but the one I mostly used and learned is a topological definition called the skeleton based on Morse theory and its extension “the persistent skeleton” based on discrete topology and persistence.
I have also studied the topology of the large-scale density field by means of excursion set theory. Instead of characterizing the statistics of the density field by its N-pt correlation functions, the focus can be put on topological (genus) and geometrical (length of filaments, peak counts) estimators that are believed to be more robust. Within this framework, I did the theory of these estimators in redshift space and to all order in non-gaussianity. With this work, I studied the so-called peak theory, Gaussian random fields, topology (Minkowski functionals, genus, . . .).
Project |03









Galaxy formation within the cosmic web
Once familiar with the beauty of the cosmic web, its geometry and its topology, a natural question which arises is whether this cosmic web is relevant to galaxies. Indeed, galactic birth and evolution take place within this large cosmic highways so that one can imagine that the properties of galaxies should have a memory of the large-scale cosmic flows in which they live.
To answer that question, I used first a DM simulation in which I measured the correlations between the spin of dark matter halos and the direction of the closest filament. It appears that small halos tend to have a spin aligned with the fila- ments while the spin of more massive halos is more likely to be perpendicular to them. With my collaborators, we proposed an explanation of this measure by means of the successive stages of structure formation (voids, walls, filaments and even- tually nodes of the cosmic web) in which halos form. This explanation was then deepened in collaboration with a master student thanks to a study of the vorticity field in simulations. The same “spin” study was later done on an hydrodynamical simulation and reveals the same signal with a mass transition from parallel to perpendicular to the filaments.
I then worked on a Lagrangian model that theoretically explains the spin geometry. The idea is to use the tidal torque theory which assumes that the spin of halos is due to a mis-alignement between its inertia tensor and the local tidal tensor but adding the ansatz that the geometry of the cosmic web nearby is anisotropic. In short, we computed, using constrained field theory, the expected spin field given a filament and a wall with some typical anisotropic geometry and found exactly the behaviour measured in simulations.
One crucial application of this work is in understanding how the large-scale coherence described above induces in- trinsic alignments of galaxies. Indeed, weak lensing is believed to be a major probe of cosmology for the coming years (Euclid, LSST, etc) but suffers from a difficult systematic effect : intrinsic alignments due to the correlations between the shapes of galaxies (II term) and between the shape of galaxies and the cosmic shear field (GI term). Because this effect depends on the non-linear gaz dynamics, the baryonic physics and the anisotropy of the cosmic web, I am convinced that hydrodynamical simulations are necessary to properly study this effect, that is why I am involved in a project in which I measured the level of intrinsic alignments in a state-of-the-art simulation run.
Just a sample of my work. To see more or discuss possible work >>